基本排序算法

发表于 | 分类于 | 0 Comments | 123

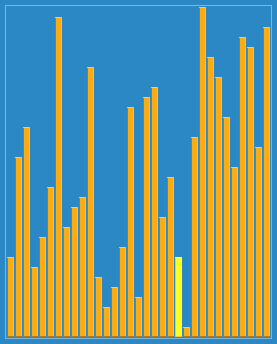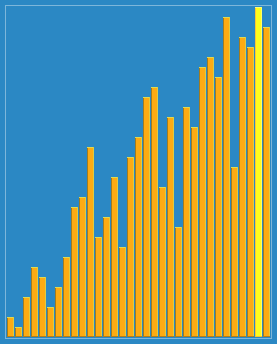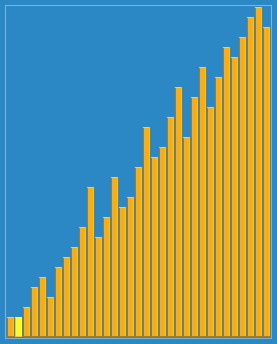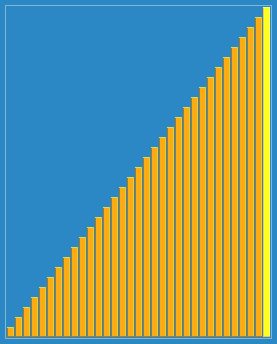
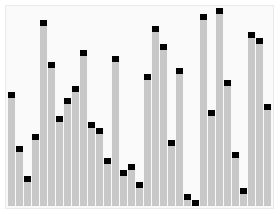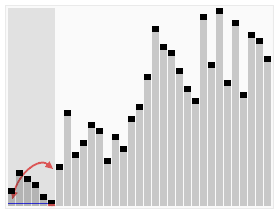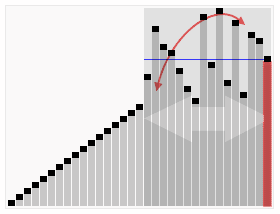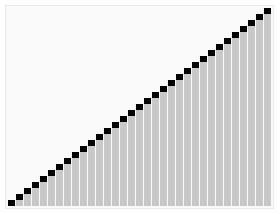
本文对基本排序算法进行总结，简述其原理，以C++实现。

  • 通用部分：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    #include <time.h>;
    using namespace std;
    #define random(x) (rand()%x)
    #define ARRAYSIZE 15
    typedef void (*SortFunc)(int data[],int);
    //数据交换
    void DataSwap(int&amp; a,int&amp; b)
    {
        if (a==b)
            return;
        a^=b;
        b^=a;
        a^=b;
    }

  • 冒泡排序

    思路：依次将剩余最小元素交换到前面
    外循环，确定剩余未排序元素的起始位置
    内循环，从后向前，相邻两个元素比较，将最小元素交换到未排序起始位置
    时间复杂度为o(n^2)，需要辅助空间o(1),稳定

    1
    2
    3
    4
    5
    6
    7
    void BubbleSort(int data[], int len)
    {
    	for(int i=0;i<len-1;++i)
    	for(int j=len-1;j>i;–j)
    	if (data[j]<data[j-1])
    	DataSwap(data[j],data[j-1]);
    }

改进冒泡排序：若一次内循环中不发生数据交换，则完成所有排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
void ImprovedBubbleSort(int data[], int len)
{
    bool flag=false;
    for (int i=0;i<len-1;++i)
    {
        flag=false;
        for (int j=len-1;j>i;–j)
            if (data[j]<data[j-1])
            {
                DataSwap(data[j],data[j-1]);
                flag=true;
            }
        if (!flag)//如果后续循环中没有发生交换的话，完成排序
            return;
    }
}


排序效果：

  • 直接选择排序

    思路：对于每个位置，分别从后面剩余元素中选择最小的元素交换至当前位置
    外循环：确定当前位置
    内循环：选择剩余最小元素
    时间复杂度为o(n^2),需要辅助空间o(1), 相比冒泡排序算法，交换次数减少 不稳定，例如5 8 5 2 9，第一次5与2交换，第一个5交换至第二个5后面
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
void SelectSort(int data[], int len)
{
    for (int i=0;i<len-1;++i)
    {
        int min=i;
        for (int j=i+1;j<len;++j)
            if (data[min]>data[j])
                min=j;
        if (min!=i)
            DataSwap(data[i],data[min]);
    }
}


排序效果：

  • 直接插入排序

    思路：依次将剩余的元素插入到已排好序的元素中
    从第二个元素开始，依次与前面的元素两两比较，若较小则交换两个元素，否则进行下一个元素的插入排序
    时间复杂度为o(n^2)，需要辅助空间o(1),稳定
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void InsertSort(int data[],int len)
{
    for (int i=1;i<len;++i)
        for (int j=i;j>0;–j)
            if (data[j]<data[j-1])
                DataSwap(data[j],data[j-1]);
            else
                break;
}


排序效果：

  • 希尔排序

    从希尔排序开始，出现时间复杂度小于o(n^2)的排序算法
    对插入排序进行改进，先子串插入排序，子串基本有序后再插入排序
    思路：将相距某个增量的元素子集进行插入排序，逐渐减小增量，再次进行子集插入排序，增量小于1时，停止。
    时间复杂度o(n*(logn)^2)，需要辅助空间o(1)，跳跃式排序，不稳定

实现1：各个子集依次处理
各个子集的第一个元素在0~gap-1位置，作为第一层for循环,各个子集依次处理, 后面两层for循环同插入排序，步长由1变为gap

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
void ShellSort(int data[], int len)
{
    int gap=len/2;
    while(gap>=1)
    {
        for (int i=0;i<gap;++i)//子集循环
        {
            for (int j=i+gap;j<len;j+=gap)//子集内插入排序
            {
                for (int k=j;k-gap>=0;k-=gap)//交换到合适位置
                {
                    if (data[k]<data[k-gap])
                        DataSwap(data[k],data[k-gap]);
                    else
                        break;
                }
            }
        }
        gap/=2;
    }
}

实现2：各个元素依次处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
void ShellSortB(int data[], int len)
{
    int gap=len/2;
    while(gap>=1)
    {
        for (int i=gap;i<len;++i)//从gap位置开始，依次遍历各个元素
        {
            for (int j=i;j-gap>=0;j-=gap)//对于各个元素，分别在其组内对其进行插入排序
            {
                if (data[j]<data[j-gap])
                    DataSwap(data[j],data[j-gap]);
                else
                    break;
            }
        }
        gap/=2;
    }
}

排序效果：

  • 堆排序

    对选择排序进行改进
    思路：先构建大顶堆(小顶堆),将第一个元素与最后元素交换，调整剩余元素形成大顶堆(小顶堆)，将第一元素与次后元素交换，反复如上操作。
    堆元素调整时从最后一个父节点开始，向前调整。
    堆排序时间复杂度为o(nlogn),辅助空间复杂度为o(1)，跳跃式排序，不稳定
    若元素从0开始，则对于节点i,其子节点为2i+1,2i+2，父节点为(i-1)/2取整；
    若元素从1开始，则对于节点i,其子节点为2i,2i+1，父节点为i/2取整。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    void HeapAdjust(int data[],int start, int end)
    {
        int temp=data[start];//暂存数据
        int k=start;//坑的位置
        for (int j=2*start+1;j<=end;j=2*j+1)
        {
            //取两个子节点中较大节点位置
            if (j<end &amp;&amp; data[j]<data[j+1])//j<end保证存在右节点
                ++j;
            //若已构成大顶堆，退出调整
            if (temp>=data[j])
                break;
            //子节点与父节点交换，形成大顶堆
            data[k]=data[j];
            k=j;
        }
        if (k!=start)
            data[k]=temp;
    }
    void HeapSort(int data[], int len)
    {
        //从最后一个父节点开始，初始化大顶堆
        for (int i=(len-1)/2;i>0;–i)
            HeapAdjust(data,i,len-1);
        //堆排序
        for(int i=len-1;i>0;–i)
        {
            DataSwap(data[0],data[i]);
            HeapAdjust(data,0,i-1);
        }
    }


排序效果：

  • 归并排序

    思路：初始认为每个元素均作为一个排好序的子集，而后将相邻两个子集进行归并排序，形成新子集，重复上述归并排序过程。
    时间复杂度o(nlogn),空间复杂度度为o(n+logn),稳定

递归实现归并排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
//两个排好序的子集归并
void Merge(int src[],int dest[],int s, int m, int e)
{
    int i=s,j=m+1,k=s;
    for (;i<=m &amp;&amp; j<=e;++k)//m为前一个子集最后一个元素位置
    {
        if (src[i]<src[j])
            dest[k]=src[i++];
        else
            dest[k]=src[j++];
    }
    while(i<=m)
        dest[k++]=src[i++];
    while(j<=e)
        dest[k++]=src[j++];
}
//对子集进行递归归并排序
void MSort(int src[],int dest[], int s, int e,int len)
{
    if (s==e)
        dest[s]=src[s];
    else
    {
        int *pTmp=new int[len];
        int m=(s+e)/2;
        MSort(src,pTmp,s,m,len);
        MSort(src,pTmp,m+1,e,len);
        Merge(pTmp,dest,s,m,e);
        delete [] pTmp;
    }
}
//调用函数
void MergeSort(int data[],int len)
{
    MSort(data,data,0,len-1,len);
}


迭代实现归并排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
void SubMerge(int src[],int dest[],int gap, int len)
{
    int i=0;
    for(;i<=len-2*gap;i+=2*gap)
    {
        Merge(src,dest,i,i+gap-1,i+2*gap-1);//每个子集内进行归并
    }
    //最后存在两个子集，但最后一个子集长度不足gap
    if (i<len-gap)
    {
        Merge(src,dest,i,i+gap-1,len-1);
    }
    else//最后剩余不足一个子集
        while(i<len)
            dest[i++]=src[i++];
}
void MergeSortB(int data[],int len)
{
    int *pTmp=new int[len];
    int k=1;
    while(k<len)
    {
        SubMerge(data,pTmp,k,len);
        k*=2;
        SubMerge(pTmp,data,k,len);
        k*=2;
    }
    delete [] pTmp;
}


排序效果：

  • 快速排序

    思路：通过一次排序，将比一个元素小的元素都放在该元素的一侧，比它大的元素都放在该元素的另一侧，对两侧元素子集同样进行上述操作
    时间复杂度为o(nlogn),空间法复杂度为o(logn),跳跃式排序，不稳定
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
void QuickSort(int data[], int start,int end)
{
    if (start<end)
    {
        int i=start,j=end;
        //零时保存参照值，该值位置形成一个坑
        int temp=data[start];
        while(i<j)
        {
            //从右往左，找到比参照值小的元素，放入坑中，找到元素位置形成新坑
            while(i<j &amp;&amp; data[j]>=temp)
                –j;
            if (i<j)
                data[i++]=data[j];
            //从左往右，找到比参照值大的元素，放入坑中，找到元素位置形成新坑
            while(i<j &amp;&amp; data[i]<=temp)
                ++i;
            if (i<j)
                data[j--]=data[i];
        }
        //将参照元素填入剩下的坑中
        data[i]=temp;
        QuickSort(data,start,i-1);
        QuickSort(data,i+1,end);
    }
}
void UseQuickSort(int data[], int len)
{
    QuickSort(data,0,len-1);
}


排序效果：

  • 测试函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
void TestSortFunc(SortFunc fp,char* desc)
{
    srand((int)time(0));
    int data[ARRAYSIZE];
    for (int i=0;i<ARRAYSIZE;++i)
    {
        data[i]=random(100);
    }
    cout<<"The origin array:"<<endl;
    for(int i=0;i<ARRAYSIZE;++i)
        cout<<data[i]<<;
    cout<<endl;
    //调用排序算法
    (*fp)(data,ARRAYSIZE);
    cout<<"The sorted array:"<<endl;
    for(int i=0;i<<ARRAYSIZE;++i)
        cout<<data[i]<<" ";
    cout<<endl<<endl;
}

  • 主函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
void main()
{
    //冒泡排序
    TestSortFunc(&amp;BubbleSort,"BubbleSort");
    //改进冒泡排序
    TestSortFunc(&amp;ImprovedBubbleSort,"ImprovedBubbleSort");
    //直接选择排序
    TestSortFunc(&amp;SelectSort,"SelectSort");
    //插入排序
    TestSortFunc(&amp;InsertSort,"InsertSort");
    //Shell排序
    TestSortFunc(&amp;ShellSort,"ShellSort");
    //Shell排序B
    TestSortFunc(&amp;ShellSortB,"ShellSortB");
    //堆排序
    TestSortFunc(&amp;HeapSort,"HeapSort");
    //递归归并排序
    TestSortFunc(&amp;MergeSort,"MergeSort");
    //非递归归并排序
    TestSortFunc(&amp;MergeSortB,"MergeSortB");
    //快速排序
    TestSortFunc(&amp;UseQuickSort,"QuickSort");
    system("PAUSE");
}

  • 测试结果

    sortResult
    小结：
    301305132036530
坚持原创技术分享，您的支持将鼓励我继续创作！